

This article is an excerpt from the Shortform book guide to "The Signal and the Noise" by Nate Silver. Shortform has the world's best summaries and analyses of books you should be reading.
Like this article? Sign up for a free trial here.
What is Bayesian Theory? How does it help forecasters make better predictions?
Named after Thomas Bayes, Bayesian Theory is one of the best ways to determine the probability of an event in the future. In his book The Signal and the Noise, Nate Silver shares two lessons you can use to correctly apply Bayesian Theory to any situation.
Let’s take a look at Bayesian Theory in detail.
Better Predictions Through Bayesian Logic
Although prediction is inherently difficult—and made more so by the various thinking errors we’ve outlined—Silver argues that it’s possible to make consistently more accurate predictions by following the principles of a statistical formula known as Bayesian Theory. Silver explains that it encourages us to think while making predictions. According to Silver, Bayesian Theory suggests that we make better predictions when we consider the prior likelihood of an event and update our predictions in response to the latest evidence.
Here, we’ll briefly describe Bayesian Theory, then we’ll explore the broader lessons Silver draws from it and offer concrete advice for improving the accuracy of your predictions.
The Principles of Bayesian Statistics
Bayesian Theory—named for Thomas Bayes, the English minister and mathematician who first articulated it—posits that you can calculate the probability of event A with respect to a specific piece of evidence B. To do so, Silver explains, you need to know (or estimate) three things:
- The prior probability of event A, regardless of whether you discover evidence B—mathematically written as P(A)
- The probability of observing evidence B if event A occurs—written as P(B|A)
- The probability of observing evidence B if event A doesn’t occur—written as P(B|not A)
Bayes’ Theorem uses these values to calculate the probability of A given B—P(A|B)—as follows:
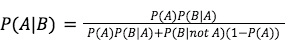
(Shortform note: This formula may look complicated, but in less mathematical terms, what it’s calculating is [the probability that you observe B and A is true] divided by [the probability that you observe B at all whether or not A is true—or P(B)]. In fact, Silver’s version of the formula (as written above) is a very common special case used when you don’t directly know P(B); that lengthy denominator is actually just a way to calculate P(B) using the information we’ve listed above.)
Bayesian Lesson #1: Consider All Possibilities
Now that we’ve explored the mathematics of Bayesian Theory, let’s look at the broader implications of its underlying logic. First, building on the principle of considering prior probabilities, Silver argues that it’s important to be open to a wide range of possibilities, especially when you’re dealing with noisy data. Otherwise, you might develop blind spots that hinder your ability to predict accurately.
To illustrate this point, Silver argues that the US military’s failure to predict the Japanese attack on Pearl Harbor in 1941 shows that it’s dangerous to commit too strongly to a specific theory when there’s scant evidence for any particular theory. He explains that in the weeks before the attack, the US military noticed a sudden dropoff in intercepted radio traffic from the Japanese fleet. According to Silver, most analysts concluded that the sudden radio silence was because the fleet was out of range of US military installations—they didn’t consider the possibility of an impending attack because they believed the main threat to the US Navy was from domestic sabotage by Japanese Americans.
Silver explains that one reason we sometimes fail to see all the options is that it’s common to mistake a lack of precedence for a lack of possibility. In other words, when an event is extremely uncommon or unlikely, we might conclude that it will never happen, even when logic and evidence dictate that given enough time, it will. For example, Silver points out that before the attack on Pearl Harbor, the previous foreign attack on US territory came in the early 19th century—a fact that made it easy to forget that such an attack was even possible.
Bayesian Lesson #2: Follow the Evidence, Not Emotions or Trends
In addition to emphasizing the importance of considering all possibilities, Bayesian logic also highlights the need to stay focused on the evidence rather than getting sidetracked by other factors such as your emotional responses or the trends you observe.
For one thing, Silver argues that when you give in to strong emotions, the quality of your predictions suffers. He gives the example of poker players going on tilt—that is, losing their cool due to a run of bad luck or some other stressor (such as fatigue or another player’s behavior). Poker depends on being able to accurately predict what cards your opponent might have—but Silver argues that when players are on tilt, they begin taking ill-considered risks (such as betting big on a weak hand) based more on anger and frustration than on solid predictions.
(Shortform note: To help keep your emotions in check, remember that getting a prediction wrong (such as by losing to an unlikely poker hand) doesn’t mean you did anything wrong—it’s not uncommon for the best possible predictions to fail simply due to luck. In fact, in Fooled By Randomness, Nassim Nicholas Taleb argues that luck is more important than skill in determining outcomes. He says that this is especially true because, in many situations, early success leads to future success, such as when a startup experiences some early good fortune that allows it to survive long enough to benefit from more good fortune down the road.)
Furthermore, Silver says, it’s important not to be swayed by trends because psychological factors such as herd mentality distort behaviors in unpredictable ways. For instance, the stock market sometimes experiences bubbles that artificially inflate prices because of a runaway feedback loop: Investors see prices going up and want to jump on a hot market, so they buy, which drives prices up even further and convinces more investors to do the same—even when there’s no rational reason for prices to be spiking in the first place.
(Shortform note: The authors of Noise explain that these kinds of feedback loops result from a psychological phenomenon known as an information cascade in which real or perceived popularity influences how people interpret information. Moreover, the authors argue that information cascades often amount to little more than luck—whichever idea receives initial support (which typically correlates with which idea is presented first) tends to be the idea that wins out regardless of its merits.)

———End of Preview———
Like what you just read? Read the rest of the world's best book summary and analysis of Nate Silver's "The Signal and the Noise" at Shortform.
Here's what you'll find in our full The Signal and the Noise summary:
- Why humans are bad at making predictions
- How to overcome the mental mistakes that lead to incorrect assumptions
- How to use the Bayesian inference method to improve forecasts






