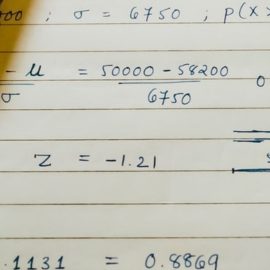This article is an excerpt from the Shortform book guide to "Naked Statistics" by Charles Wheelan. Shortform has the world's best summaries and analyses of books you should be reading.
Like this article? Sign up for a free trial here .
What are inferential statistics? How are inferential statistics applied in real life?
Inferential statistics are a powerful research tool due to a statistics tenet called the central limit theorem. The central limit theorem states that the mean of a representative sample will be close to the mean of the larger population. Therefore, we can confidently make inferences about a population from a sample or about a sample from a population, and we can compare samples to each other.
In this article, we’ll explore inferential statistics examples in real life.
Making Inferences About a Population From a Sample
We can use samples to glean reliable information about an entire population if we know the population’s mean and standard deviation for the variable we’re interested in. Since collecting data on an entire population is often neither feasible nor possible, the central limit theorem allows us to ask research questions that would otherwise be unanswerable.
(Note: Wheelan explains that 30 is the minimum sample size for reliable statistics, although there are mathematical fixes for smaller sample sizes.)
For example, many people believe that participating in gymnastics at a young age stunts girls’ growth. You can’t possibly collect data on every female gymnast to answer this question. Still, with the central limit theorem and inferential statistics, you can use a sample of gymnasts to test the null hypothesis that: “There is no difference in height as an adult between female gymnasts and non-gymnasts.”
| Explicit Sampling Methods Including how samples are collected in a study is an important feature of ensuring replicability, a feature of high-quality research. If a study is replicable, other researchers can verify results, and trust in the study increases. In contrast, no one can verify the results when a study isn’t replicable, and the study becomes less trustworthy. Replication is why scientific papers include a materials and methods section. For example, as an ornithologist reading a study about local bird populations, you might raise an eyebrow if the study reports a much higher population density for a particular species than you’d estimate for your region. Without an explicit description of sampling techniques, you’d have no idea how the researchers arrived at those numbers. Did they count the number of nests in a given quadrant? Did they sit in one spot for a given amount of time and count birds? Did they play bird sounds and tally responses? Without context for their sampling methods, the researchers’ results might become meaningless to your critical eye. |
Making Inferences About a Sample From a Population
Since we know that samples look like their underlying population, we can also use the central limit theorem to make inferences about the composition of a sample taken from a given population. For example, say the organizers of a fun-run want to know how long they should give participants to finish their two-mile course. They can’t know the exact pace of each participant who will show up at the race, but they can use average running paces from the general population to assume that the majority of participants will finish the course between the 20- and 30-minute mark.
| Marketing and Data A noteworthy inferential statistics example in real life is targeted marketing. Data shows that female consumers make up to 80% of all purchasing decisions and that women make the plurality of couples’ decisions. Therefore, a great deal of current marketing targets women rather than men, with the logic being that ads reaching a sample of female shoppers will yield higher returns than ads reaching a sample of male shoppers. |
Making Inferences to Connect Samples
Since samples look like their population, we would expect two samples taken from the same population to look like each other. When they don’t, the two samples have significant underlying differences in terms of the variable we’re studying.
For example, a researcher’s null hypothesis might be: “There is no difference in lung cancer rates between asbestos factory workers and the general population.” The researcher could collect data on 100 asbestos workers and 100 people from the general population and compare cancer rates. If the rates of lung cancer were significantly different between the two samples, it would be a powerful indicator that the two samples came from “different populations” with respect to the variable we’re studying (in other words, as far as lung cancer rates are concerned, asbestos workers are in a different population than the public).
| Using Samples to Generate Categories Wheelan explains that statistics can help researchers group people into different “populations” pertaining to a specific research question. While these groupings may be statistically sound and collectively beneficial, like all statistics, they can lack the nuance necessary to understand individuals. For example, a highly publicized and controversial way that biomedical samples are used to categorize people is using the average testosterone levels of men and women to disqualify some female athletes from athletic competition. Testosterone is widely considered to be a performance-boosting hormone, and as such, having “extra” testosterone as an athlete is considered cheating. Therefore, women whose testosterone levels are well above the female mean are considered to be in a different population than other female athletes and can be barred from competition. Many people argue that barring women from competition on the basis of testosterone is a form of legal discrimination. While a female with high levels of testosterone might be a statistical rarity, Wheelan reminds us that statistically improbable events happen all the time. With roughly 7.75 billion people in the world, there will be many women whose levels of testosterone naturally fall well outside the average female range. Many argue that since anomalously tall individuals are not barred from playing basketball, and people with anomalously long torsos are not barred from competitive swimming, the rationale behind this decision is debatable. |
Standard Error
We noted above that according to the central limit theorem, the means of large representative samples will be “close” to the mean of the underlying population. More specifically, the central limit theorem states that sample means form a normal distribution around the population mean. In other words, if we took enough samples, the means of those samples would form a perfectly symmetrical bell curve around the true mean of the population.
For instance, let’s say you took a random sample of 100 people, measured their heights, and got a mean height of 5 feet 7 inches. Then you repeated the experiment with a different group of 100 people and got a mean height of 5 feet 8 inches. If you repeated the experiment 50 times with 50 different samples, then plotted those 50 sample means on a graph, they would form a normal bell curve centering on the true average height for the entire population.
Since data is distributed predictably around the mean in a normal distribution, we use the same principles we covered in our discussion of standard deviation to describe how close a particular sample mean is to the population mean. However, when we’re discussing the distribution of sample means around a population mean, we use a statistic called standard error rather than the standard deviation. The standard error is the standard deviation of sample means around a population mean.
As a reminder, in a normal distribution, 68.2% of data points will fall within one standard deviation of the mean, 95.4% of data points fall within two standard deviations of the mean, and 99.7% of data points fall within three standard deviations of the mean. Therefore, for a group of sample means around a population mean, 68.2% of sample means will fall within one standard error of the population mean and so on.
Using our height example, say the mean population height is 5’8”, and we calculate a standard error of 1 inch for our sample means. A sample with a mean height of 5’10” would be two standard errors taller (on average) than the population mean height. Another way to say this is that this sample mean is larger than 95.4% of all other sample means.
| The Benefits of a Large Sample Wheelan explains that the standard error is calculated by dividing the standard deviation of the sample by the square root of the sample size (number of data points). Because the size of the sample is in the denominator in the standard error equation, Wheelan notes that large sample sizes reduce the standard error. However, because the equation uses the square root of the sample size, a large increase in sample size corresponds to a much smaller decrease in standard error. In our height example above, for instance, we had a sample height of 5 feet 7 inches and a standard error of one inch from a sample of 100 people. Provided the standard deviation of the sample remains consistent, if we wanted to decrease our standard error to half an inch, we would have to sample 400 people. If we wanted to reduce our standard error to a tenth of an inch, we would have to sample 10,000 people. As we can see, the larger the sample, the more precisely we can pinpoint how close our samples are to the true population mean. |
Polling With the Central Limit Theorem
Another powerful use of inferential statistics involves polling. Since polling involves making inferences about a population from a sample, the central limit theorem allows us to use polls to predict public opinion. In polls, our “sample mean” is the percent of survey respondents who indicate that they’ll vote a certain way, and our “population mean” is the actual percent of people who will vote that same way on election day.
For example, say you conduct a survey to see whether voters will approve a ballot measure to build a local dog park. Your sample is the people who respond to your survey. Your “sample mean” is the number of respondents who indicate that they’ll vote “yes” on election day. Your population mean is the number of residents who will actually vote “yes” on election day.
The standard error and normal distribution allow us to gauge how confident we can be in our polling results. The standard error of a poll is also a percent. We can use the standard error to establish a range around our polling results within which we expect the true election results to fall, and our normal distribution to express how confident we are in that range. We’ll illustrate this with our dog park example.
Say that 55% of your dog park survey respondents indicate that they’ll vote “yes,” and say that you calculate the standard error of your survey to be 4%. The range of “yes” responses within one standard error of your poll is 51% to 59%. Using the normal distribution, you know that 68.2% of the time your polling results will be within one standard error of the true election results. Since 51% is over half the votes, you can be 68.2% confident that the dog park will pass with between 51% and 59% of the votes.
(Note: If a range of two standard errors from our poll results was still above 50% we would be able to use the normal distribution to say that we were 95.4% confident the measure would pass, and if a range of three standard errors from our poll results were still above 50%, we would be able to say that we’re 99.7% confident that the dog park will pass.)
| Polling and the US Census The US census is an example of how the central limit theorem allows pollsters and researchers to make back and forth inferences between a sample and a population. The census provides the most accurate data possible about the US population. Using this population-level data, pollsters and researchers can compare the results of their samples to the overall population and calibrate their sampling results with known population values. For example, if your research showed much smaller families in your sampling area than indicated by the census, you might adjust the family size of your sampling results to fit the census count better. Calibrating polling results with census data is common practice because it’s assumed that polls will be inaccurate to varying degrees. Using census data to more accurately weight certain demographics can help pollsters get closer to the “right answer” (the population mean). In other words, census data helps pollsters organize their data into a more representative sample. Working in the opposite direction, sample data from the American Community Survey sent to portions of the US population each year helps update population-level census data between census counts. |

———End of Preview———
Like what you just read? Read the rest of the world's best book summary and analysis of Charles Wheelan's "Naked Statistics" at Shortform .
Here's what you'll find in our full Naked Statistics summary :
- An explanation and breakdown of statistics into digestible terms
- How statistics can inform collective decision-making
- Why learning statistics is an exercise in self-empowerment