
This article is an excerpt from the Shortform summary of "The Black Swan" by Nassim Taleb. Shortform has the world's best summaries of books you should be reading.
Like this article? Sign up for a free trial here .
What is a Gaussian curve? In which situations can it accurately describe the world? Where does it fail, and what are its limits?
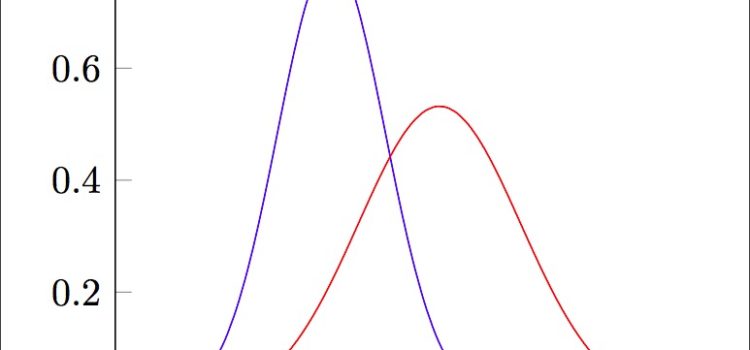
The Gaussian curve is another name for the classic bell curve, or normal distribution curve. It’s named after German mathematician Carl Friedrich Gauss, and it describes many phenomena accurately.
We’ll look at where the Gaussian curve is accurate and where (and why) it fails.
The Limits of the Gaussian Curve
The classic bell curve—which is also called the normal distribution curve, “Gaussian distribution,” or Gaussian curve, after German mathematician Carl Friedrich Gauss—is an accurate description of Mediocristan phenomena, but it is dangerously misleading when it comes to Extremistan.
Consider human height, an eminently Mediocristan phenomenon. With every increase or decrease in height relative to the average, the odds of a person being that tall or short decline. For example, the odds that a person (man or woman) is three inches taller than the average is 1 in 6.3; 7 inches taller, 1 in 44; 11 inches taller, 1 in 740; 14 inches taller, 1 in 32,000.
It’s important to note that the odds not only decline as the height number gets further and further away from the average, but they decline at an accelerating rate. For example, the odds of someone being 7’1” are 1 in 3.5 million, but the odds of someone being just four inches taller are 1 in 1 billion, and the odds of someone being four inches taller than that are 1 in 780 billion! Human height is accurately described by the Gaussian curve (normal distribution curve).
Now consider an Extremistan phenomenon like wealth. In Europe, the probability that someone has a net worth higher than 1 million euros is 1 in 62.5; higher than 2 million euros, 1 in 250; higher than 4 million, 1 in 1,000; higher than 8 million, 1 in 4,000; and higher than 16 million, 1 in 16,000. The odds decrease at a constant, rather than accelerating, rate, indicating that their distribution doesn’t conform to a Gaussian curve.
(Note: The European wealth statistics cited above aren’t precise, but they illustrate the central point: that wealth is scalable and does not look like a bell or Gaussian curve.)
The upshot is that in Extremistan, as the name suggests, extreme events have much better odds of occurring than in Mediocristan. Simply put, the Gaussian curve does not apply.
The Mistakes of Adolphe Quételet
Adolphe Quételet (1796–1874) was a French mathematician who developed the idea of the “average human” (l’homme moyen) through the use of “means”—golden averages that represented the ideal human form.
At first, his inquiries were limited to human beings’ physical characteristics—height, weight, newborn weight, chest size—but before long, he began to seek averages in the social realm by studying human habits and morals. Quételet developed bell curves, or Gaussian curves, to describe humans’ deviance—literally—from both physical and moral norms.
Although Quételet’s ideas were influential in his historical moment, there were skeptics. Augustin Cournot, a fellow mathematician and philosopher, pointed out that social averages would necessarily depend on exactly whom and what attribute was being studied. An obvious example is human diet: If you were trying to determine the amount of seafood an average human consumes, you might get vastly different measurements if you were surveying inland populations versus coastal ones, or populations whose cultural traditions included a seafood-heavy diet.
In our contemporary moment, the most egregious misuse of Gaussian curves can be found among economists and financial-industry analysts. Most economists, including many Nobel Prize–winners, treat financial markets as though they hail from Mediocristan when, in fact, they’re from Extremistan.
A stunning example of economists’ misinterpretation of the market and Gaussian curves came in 1998, with the collapse of Long-Term Capital Management (LCTM), a hedge fund that included among its founding partners two Nobel Prize–winners, Myron Scholes and Robert C. Merton (Robert K. Merton’s son). Scholes and Merton won their Nobel Prize for a theory of stock option pricing; the theory, however, was based on a Gaussian model of the market that excluded the possibility of Black Swans.
When markets were disrupted by the Asian financial crisis of 1997 and the Russian financial crisis of 1998—a one-two punch of Black Swans—Scholes and Merton’s theory was revealed for the fantasy it was. The twin crises resulted in a crushing $4.6 billion loss for LCTM in fewer than four months. The firm had to be bailed out by a consortium of private banks, at the behest of the Federal Reserve.
The problem is that economists’ models are thoroughly Platonified: self-consistent, but bearing almost no resemblance to reality. Economists are like philosopher John Locke’s madmen: they reason “correctly from erroneous premises.” The Gaussian curve is part of the erroneous premise.
Say you want to assess the risk of a stock portfolio, and you know that, based on past data, the worst-case scenario is a -5% move once every 2 years. With a power of 2—remember that the power is estimated—you can assume that a -10% move will happen once every 8 years (2^2=4) and a -20 percent move will happen once every 32 years. (For scale, in the 1987 crash, the U.S. stock market lost almost 23% of its value, an impossibility according to Gaussian economic models.) With fractal/power-law distributions, a 1000-year flood can become a 100-year one, and a 100-year one can become a 10-year one.
———End of Preview———

Like what you just read? Read the rest of the world's best summary of "Black Swan" at Shortform . Learn the book's critical concepts in 20 minutes or less .
Here's what you'll find in our full Black Swan summary :
- Why world-changing events are unpredictable, and how to deal with them
- Why you can't trust experts, especially the confident ones
- The best investment strategy to take advantage of black swants