How Bayesian Principles Help Us Make Better Predictions

This article is an excerpt from the Shortform book guide to "The Signal and the Noise" by Nate Silver. Shortform has the world's best summaries and analyses of books you should be reading.

Like this article? Sign up for a free trial here.

What are the principles of Bayes’ Theorem? How can they help you calculate the probability of an event?

Bayes’ Theorem suggests that you make better predictions when you consider the prior likelihood of an event and update your predictions in response to the latest evidence. Nate Silver discusses how the theorem encourages you to think while making predictions.

Let’s look at the two Bayesian principles that can help you think better.

The Principles of Bayesian Statistics

Bayes’ Theorem—named for Thomas Bayes, the English minister and mathematician who first articulated it—posits that you can calculate the probability of event A with respect to a specific piece of evidence B. He explains how to make this calculation and shares two Bayesian principles that can

To calculate the probability of event A with respect to evidence B, Silver explains, you need to know (or estimate) three things:

The prior probability of event A, regardless of whether you discover evidence B—mathematically written as P(A)
The probability of observing evidence B if event A occurs—written as P(B|A)
The probability of observing evidence B if event A doesn’t occur—written as P(B|not A)

Bayes’ Theorem uses these values to calculate the probability of A given B—P(A|B)—as follows:

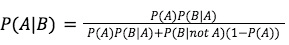
(Shortform note: This formula may look complicated, but in less mathematical terms, what it’s calculating is [the probability that you observe B and A is true] divided by [the probability that you observe B at all whether or not A is true—or P(B)]. In fact, Silver’s version of the formula (as written above) is a very common special case used when you don’t directly know P(B); that lengthy denominator is actually just a way to calculate P(B) using the information we’ve listed above.)

Principle #1: Consider the Prior Probability

To illustrate how Bayes’ Theorem works in practice, imagine that a stranger walks up to you on the street and correctly guesses your full name and date of birth. What are the chances that this person is psychic? Say that you estimate a 90% chance that if this person is psychic, they’d successfully detect this information, whereas you estimate that a non-psychic person has only a 5% chance of doing the same (perhaps they know about you through a mutual friend). On the face of it, these numbers seem to suggest a pretty high chance (90% versus 5%) that you just met a psychic.

But Bayes’ Theorem reminds us that prior probabilities are just as important as the evidence in front of us. Say that before you met this stranger, you would’ve estimated a one in 1,000 chance that any given person could be psychic. That leaves us with the following values:

P(A|B) is the chance that a stranger is psychic given that they’ve correctly guessed your full name and date of birth. This is what you want to calculate.
P(A) is the chance that any random stranger is psychic. We set this at one in 1,000, or 0.001.
P(B|A) is the chance that a psychic could correctly guess your name and date of birth. We set this at 90%, or 0.9.
P(B|not A) is the chance that a non-psychic could correctly guess the same information. We set this at 5%, or 0.05.

Bayes’ Theorem yields the following calculation:

P(A|B)= 0.001 x 0.9/0.001 x 0.9 + 0.05(1-0.001) = .0009/.05085 = 0.017699

That’s an approximately 1.77% chance that the stranger is psychic based on current evidence. In other words, despite the comparatively high chances that a psychic stranger could detect your personal information while a non-psychic stranger couldn’t, the extremely low prior chance of any stranger being psychic means that even in these unusual circumstances, it’s quite unlikely you’re dealing with a psychic.

(Shortform note: In Superforecasting, Tetlock sums all this math up in plain language by explaining that Bayesian thinkers form new beliefs that are a product of their old beliefs and new evidence. He also borrows Kahneman’s description of this process as taking an “outside view,” because when you start from base probability rates (such as the odds that any random stranger is psychic), you put yourself outside of your specific situation and you’re less likely to be unduly swayed by details that feel compelling but have only limited statistical significance (such as the stranger’s unlikely guesses about your personal information).)

Principle #2: Update Your Estimates

Silver further argues that Bayes’ Theorem highlights the importance of updating your estimates in light of new evidence. To do so, simply perform a new calculation whenever you encounter new facts and take the results of the previous calculation as your starting point. That way, your estimates build on each other and, in theory, gradually bring you closer to the truth.

For example, imagine that after guessing your name and birth date, the stranger proceeds to read your thoughts and respond to what you’re thinking before you say anything. Perhaps you’d once again set the chances of a psychic doing so (P(B|A)) at 90% versus 5% for a non-psychic (P(B|not A))—perhaps the stranger is a very lucky guesser. But this time, instead of setting the prior chance of the stranger being psychic (P(A)) at one in 1,000, you’d set it at your previously calculated value of 0.017699—after all, this isn’t any random stranger, this is a random stranger who already successfully guessed your name and birth date. Given this prior evidence and the new evidence of possible mind-reading, the new calculation yields:

P(A|B)=0.017699 x 0.9/0.017699 x 0.9 + 0.05(1-0.017699) = 0.0159291/0.06504415 = 0.24489674

Now you have an approximately 24.49% chance that you’re dealing with a psychic—that’s because, in non-mathematical terms, you updated your previously low estimate of psychic likelihood to account for further evidence of potential psychic ability—and logically enough, even your unlikely conclusion becomes likelier with more evidence in its favor.

(Shortform note: In other words, one of the benefits of Bayesian thinking is that it accounts for your prior assumptions while also letting you know when those assumptions might be wrong. In Smarter Faster Better, Charles Duhigg explains how Annie Duke (Thinking in Bets) applied this kind of thinking during her professional poker career. Duke could often size up opponents at a glance by observing, for example, that 40-year-old businessmen often played recklessly. But to keep her edge, she had to stay alert to new information—such as a 40-year-old businessman who plays cautiously and rarely bluffs. Otherwise, her initial assumptions might lead her to bad decisions.)

How Bayesian Principles Help Us Make Better Predictions