Resumen del libroEstadística al desnudo, de Charles Wheelan

Resumen de una páginaResumen de una página del libro «Naked Statistics»

Wheelan comienza *Naked Statistics* reconociendo que, en ocasiones, le costaba ver la relevancia de lo que aprendía como estudiante de matemáticas. Por ello, en el libro sitúa la relevancia de la estadística en primer plano, y articula su análisis de cada concepto estadístico en torno a las razones por las que debemos conocerlo. Y lo que es mejor, Wheelan demuestra que la estadística no tiene por qué resultar intimidante, al explicar los fundamentos matemáticos que la sustentan en términos sencillos y ilustrar los conceptos con ejemplos cercanos, relevantes e incluso divertidos.

Esta guía se centra principalmente en dos temas principales de *Naked Statistics*. En primer lugar, explicamos qué significan muchas estadísticas comunes, cómo interpretarlas y por qué son importantes. Al igual que Wheelan, utilizamos ejemplos reales y ficticios para contextualizar cada estadística tratada. En segundo lugar, analizamos el análisis que hace Wheelan de las consecuencias del sesgo y de la aplicación y la interpretación erróneas de las estadísticas, con el fin de defender que todo el mundo debería adquirir conocimientos básicos de estadística.

Las estadísticas organizan los datos

Nos basamos en los datos para entender el mundo, pero sin estadísticas, los conjuntos de datos serían prácticamente inútiles. Imagina que le preguntas a un vendedor de coches qué consumo tiene un vehículo y te entrega una hoja de cálculo de 100 páginas con los kilómetros recorridos individualmente por ese coche y la cantidad de combustible que ha consumido en cada kilómetro. Aunque la hoja de cálculo sea exhaustiva, resulta bastante inútil si lo que esperabas era una respuesta rápida. Con la estadística, podemos tomar conjuntos de datos poco manejables y transformarlos en valores significativos y útiles, como el consumo medio por kilómetro.

Las estadísticas que resumen conjuntos de datos se denominan estadísticas descriptivas. Dos de las estadísticas descriptivas más conocidas y utilizadas son la media (el promedio) y la mediana (el número que se encuentra en el centro cuando se ordenan todos los datos numéricamente). La media y la mediana se denominan medidas de tendencia central y, aunque ambas nos informan sobre el «punto medio» de un conjunto de datos, Wheelan explica que pueden transmitir mensajes muy diferentes. Con unos conocimientos básicos de estadística, podemos aprender cuándo utilizar una u otra y detectar cuándo alguien podría estar indicando la media en lugar de la mediana (o viceversa) para favorecer sus propios intereses.

Imaginemos que las autoridades de una playa ficticia recopilan datos sobre el número de picaduras de medusa que sufren los bañistas cada semana durante el verano. Los datos podrían tener un aspecto similar al siguiente:

(Nota breve: En este ejemplo, el conjunto de datos está ordenado de forma natural, por lo que no es necesario ordenarlo para calcular la mediana.)

El promedio de picaduras de medusa es de 42. La mediana es cero. Las autoridades de la playa podrían decir:

A) «¡Ven a nuestra playa! ¡El promedio de picaduras por cada 500 bañistas a lo largo del verano es de solo 42!»

o

B) «¡Ven a nuestra playa! ¡El promedio de picaduras semanales durante todo el verano es de cero!»

Ninguna de estas afirmaciones es incorrecta, pero transmiten un mensaje diferente a los posibles bañistas. Las autoridades de la playa seguramente promocionarán la opción B en lugar de la A, ya que la opción B hace que la playa parezca más atractiva. Como estudiantes de estadística perspicaces, debemos preguntarnos qué medida de tendencia central refleja mejor la «historia» del conjunto de datos y ser conscientes de que ninguna estadística por sí sola puede transmitir plenamente la complejidad del mundo real.

La utilidad de la tendencia central

Las medidas de tendencia central son fundamentales para la forma en que interpretamos y comunicamos los datos. Sin embargo, tal y como advierte Wheelan y pone de manifiesto nuestro ejemplo de las medusas, si no se utilizan con cuidado, pueden resultar inútiles o incluso peligrosas.

Una charla TED titulada«El mito de la media»pone de relieve cómo la aplicación errónea de la tendencia central afectó a la Fuerza Aérea de los Estados Unidos en la década de 1950. A pesar de contar con pilotos bien entrenados y con los aviones más avanzados de la época, la Fuerza Aérea no estaba satisfecha con el rendimiento de los pilotos. Las investigaciones sobre las dimensiones de miles de pilotos revelaron que las cabinas diseñadas para el piloto de «tamaño medio» no se adaptaban bien a ningún piloto, y que las cabinas mal ajustadas impedían a los pilotos volar al máximo de sus capacidades. En respuesta a ello, la Fuerza Aérea cambió el enfoque de su diseño, pasando de fabricar cabinas que se ajustaran a la persona media a fabricar cabinas que pudieran adaptarse a las dimensiones humanas más extremas. Este cambio mejoró el rendimiento de los pilotos existentes y permitió a la Fuerza Aérea reclutar el grupo de pilotos de caza más diverso del mundo.

La lección que se desprende de este ejemplo es que una herramienta diseñada para el usuario medio probablemente no sea la ideal para nadie. En muchos casos, como en el de unas tijeras, podemos aceptar fácilmente este compromiso. Sin embargo, cuando se trata de situaciones que pueden cambiar la vida, como pilotar un avión, tal vez convenga replantearse los diseños basados en un perfil medio.

Las estadísticas revelan y describen relaciones

Las estadísticas descriptivas también pueden poner de manifiesto y describir las relaciones entre las variables de un conjunto de datos. Como explica Wheelan, **analizar la correlación entre dos variables puede indicarnos si un cambio en...

Resumen de «Naked Statistics » Introducción breve

Wheelan explica que aprender estadística puede convertirnos en consumidores más críticos de la información y ayudarnos a tomar decisiones fundamentadas. Como estudiantes de estadística, podemos aprender a evaluar la información que se nos presenta en campañas políticas y de marketing, en las noticias, en publicaciones científicas, etc., y situar esa información en un contexto útil. Aprender estadística también nos ayudará a detectar usos engañosos o erróneos de los datos y las estadísticas, en lugar de dejarnos engañar por ellos.

Gracias a Charles Wheelan, las estadísticas ya no tienen por qué resultar intimidantes. «Naked Statistics» explica los fundamentos matemáticos de las estadísticas en un lenguaje sencillo y ilustra los conceptos estadísticos con ejemplos cercanos, relevantes e incluso divertidos. Los lectores también se benefician de las reflexiones sociopolíticas que ofrece el libro, ya que Wheelan recurre a anécdotas de la vida real para explorar cómo las estadísticas pueden influir en la toma de decisiones colectivas.

Acerca del autor

Charles J. Wheelan es profesor del Dartmouth College y antiguo profesor de la Universidad de Chicago, especializado en políticas públicas. Es licenciado por el Dartmouth College, tiene un máster en Asuntos Públicos por la Universidad de Princeton y un doctorado en Políticas Públicas por la...

Resumen de «Naked Statistics» ¿Por qué aprender estadística?

La segunda parte del título de *Naked Statistics* , *Stripping the Dread From the Data*(Despojando a los datos de su temible reputación), explica a los lectores por qué el libro de Wheelan es una buena opción si sienten curiosidad por la estadística pero les intimida un libro basado en las matemáticas. Wheelan, autor de éxitos de ventas del New York Times, profesor titular en el Dartmouth College y antiguo profesor titular en la Universidad de Chicago, utiliza sus habilidades como docente y narrador para hacer que el análisis de datos resulte cercano, fácil de entender y entretenido.

Como explica Wheelan, la estadística es una herramienta poderosa para resumir información y extraer conclusiones a partir de los datos. Señala que, sin ella, a la gente le resultaría difícil extraer sentido de la ingente cantidad de datos que nuestra sociedad genera a diario. Por lo tanto, la estadística convierte los datos en algo significativo y útil.

Los conocimientos que obtenemos gracias a la estadística contribuyen al funcionamiento de la sociedad tal y como la conocemos. Por ejemplo, las mejores prácticas en medicina y educación se establecen mediante análisis estadísticos de los datos. Los legisladores utilizan los datos para fundamentar sus políticas. Los aficionados al deporte utilizan los datos para debatir sobre la habilidad y el potencial de sus jugadores y equipos favoritos, y la lista podría seguir. Utilizamos la estadística de tantas formas que Wheelan nos recuerda que está presente en nuestra vida cotidiana...

Resumen de «Naked Statistics»: uso de la estadística descriptiva para describir las medidas de tendencia central

Ahora que hemos visto por qué es importante aprender estadística, vamos a repasar algunos términos y conceptos básicos de estadística, empezando por la estadística descriptiva. Como su nombre indica, la estadística descriptiva toma la información de un conjunto de datos y la resume en una cifra significativa, como una media o un percentil.

Wheelan explica que, al utilizar estadísticas descriptivas para resumir datos, siempre nos enfrentamos a una disyuntiva entre la complejidad y la utilidad. Cada vez que tomamos datos del mundo real y los condensamos en un único valor, obtenemos una visión general de los datos en su conjunto, pero perdemos parte de los matices y la «historia» que hay detrás de ellos.

Por ejemplo, supongamos que la escuela primaria de tu localidad ha puesto en marcha un nuevo programa de lectura que ha mejorado las habilidades lectoras generales de los alumnos en un 15 %. ¡Hurra! Sin embargo, un análisis más detallado podría revelar que esas mejoras se concentraron en los alumnos de familias con altos ingresos, mientras que las habilidades lectoras de los alumnos de familias con bajos ingresos se mantuvieron prácticamente igual. A la luz de este panorama más completo, parece claro que es necesario modificar el programa.

Como muestra nuestro ejemplo del programa de lectura, las estadísticas descriptivas que elegimos al resumir los datos tienen un impacto decisivo en la historia que...

Resumen de «Naked Statistics»: uso de la estadística descriptiva para resumir la distribución de los datos

Como hemos visto, las medidas de tendencia central no nos ofrecen una visión completa de un conjunto de datos. Podemos obtener una imagen más clara de ese conjunto combinando la tendencia central con una descripción de la distribución de los datos.

La distribución normal

La distribución normal es un concepto fundamental en estadística. Una distribución normal se refiere a un conjunto de datos que, al representarse gráficamente como una distribución de frecuencias (una representación visual de los datos en la que la altura de las barras representa el número de veces que se produce un resultado específico), forma una curva de campana perfectamente simétrica en torno a la media.

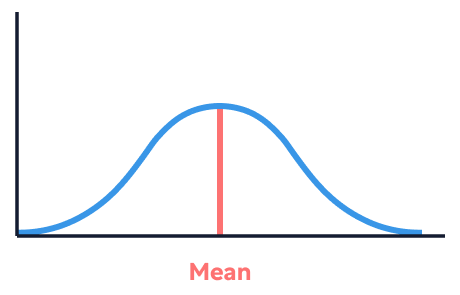
(Ten en cuenta que la media y la mediana serán iguales en una distribución perfectamente simétrica.)

Cuando un conjunto de datos tiene el mismo aspecto a ambos lados de la media, decimos que es simétrico. Las distribuciones simétricas nos resultan intuitivamente familiares porque, como explica Wheelan, se dan constantemente en la vida real. Por ejemplo, la mayoría de los bebés empiezan a gatear entre los seis y los doce meses, con una media de unos nueve meses. Algunos gatearán antes de los seis meses y otros lo harán después de los doce, pero el pico de nuestra frecuencia...

Ejercicio breve: Detecta las estadísticas engañosas

Wheelan explica que cualquiera que tenga la voluntad y un programa informático adecuado puede realizar análisis estadísticos. Esta accesibilidad, unida a la facilidad y rapidez con que se comparte la información en nuestra cultura orientada a la tecnología, hace que las estadísticas engañosas se cuelen fácilmente en nuestras vidas e influyan en nuestras opiniones o decisiones.

Piensa en la última vez que leíste o te contaron una estadística que te llamó la atención. ¿Cuál fue tu primera impresión sobre la validez de esa estadística?

Resumen de «Naked Statistics»: El uso de la probabilidad para tomar decisiones

La probabilidad es otra forma de utilizar la estadística descriptiva para tomar decisiones fundamentadas.

La probabilidad es una relación matemática que indica la posibilidad de que se produzca un acontecimiento concreto frente a todos los demás resultados posibles. La probabilidad nos permite gestionar la incertidumbre midiendo los riesgos y poniendo en perspectiva los posibles resultados. Wheelan explica que comprender la probabilidad puede resultar especialmente relevante para nuestra vida cotidiana, ya que tomamos decisiones basadas en nuestra percepción de la probabilidad constantemente.

Sin embargo, nuestra percepción de los posibles resultados suele ser matemáticamente irracional. Por ejemplo, la probabilidad de sufrir un accidente de tráfico mientras conducimos hacia la playa es mucho mayor que la probabilidad de que nos ataque un tiburón una vez allí, pero a menudo —de forma irracional— tememos más el riesgo que supone el tiburón.

A continuación, analizaremos algunos de los conceptos básicos y las aplicaciones de la probabilidad.

La probabilidad no es intuitiva

Hay varias razones que explican nuestra percepción matemáticamente irracional de la probabilidad, entre ellas:

• Sesgo de confirmación: es lo que ocurre cuando nos centramos en lo que esperamos e ignoramos lo...

Resumen de «Naked Statistics »: «Supuestos seguros » en la estadística inferencial

Hemos visto cómo la estadística descriptiva nos ayuda a resumir y describir datos, caracterizar relaciones y hacer predicciones. A continuación, pasaremos a la estadística inferencial, que nos permite extrapolar más allá de los datos que recopilamos y hacer inferencias sobre cómo funciona el mundo.

Wheelan describe la estadística inferencial como la combinación de datos y probabilidad. Al igual que la probabilidad nunca garantiza un resultado, tampoco hay respuestas definitivas en la estadística inferencial. Más bien , la estadística inferencial nos ayuda a utilizar lo que sabemos para formular hipótesis fundamentadas matemáticamente sobre lo que queremos saber.

La estadística inferencial no ofrece un mecanismo

Como explica Wheelan, la estadística inferencial es muy eficaz a la hora de poner de manifiesto y describir relaciones, pero en realidad no puede demostrar nada por sí sola, ya que se basa exclusivamente en datos numéricos que no pueden captar la complejidad del mundo real. En otras palabras, la estadística inferencial nos da una razón de peso para creer que dos variables están relacionadas, pero no nos proporciona un [mecanismo para ello...

Resumen de «Naked Statistics»: Encontrar respuestas con el análisis de regresión

Todas las estadísticas y los escenarios de recopilación de datos que hemos analizado hasta ahora han sido relativamente sencillos, ya que se centran principalmente en una sola variable. Sin embargo, Wheelan sostiene que muchas cuestiones de investigación de importancia social son «complejas», con variables entrelazadas que abarcan períodos de tiempo excesivamente largos.

Por ejemplo, supongamos que quieres saber si la exposición a una sustancia química concreta (la llamaremos sustancia química X) está relacionada con un mayor riesgo de desarrollar cáncer. No es posible diseñar un estudio de investigación para responder a esta pregunta, ya que exponer a un grupo de personas a una sustancia química que se sospecha que causa cáncer sería éticamente problemático. Además, hay un sinfín de otras variables, además de la exposición química, que influyen en el riesgo de desarrollar cáncer: el tabaquismo, la genética, la dieta, el ejercicio, etc. Por último, el riesgo de desarrollar cáncer suele medirse a lo largo de toda la vida. Es comprensible que los investigadores quieran respuestas en el transcurso de sus propias vidas.

En situaciones de investigación «complejas», una herramienta de estadística inferencial denominada «análisis de regresión» puede ayudarnos a deducir relaciones entre variables que, de otro modo, no podríamos estudiar. **El análisis de regresión cuantifica...

Ejercicio breve: Diseña un estudio

Ahora que hemos hablado del potencial y las dificultades de la estadística inferencial, piensa en una pregunta que te interese y en cómo podrías utilizar la estadística para responderla.

¿Cuáles son las variables independientes y dependientes de este estudio? ¿Cuáles son las hipótesis nula y alternativa?

Resumen de «Naked Statistics »: Datos de calidad : la base de unas estadísticas fiables

Hemos analizado algunas de las estadísticas más utilizadas con las que probablemente nos encontremos en nuestra vida cotidiana. Sin embargo, saber cómo realizar análisis estadísticos es solo una pequeña parte del proceso estadístico en su conjunto. Wheelan explica que, en cierto sentido, la «parte matemática» de la estadística es la más fácil, ya que la mayoría de los análisis estadísticos los hacemos en un ordenador, y las fórmulas estadísticas en sí mismas son fijas y fáciles de consultar. Por lo tanto, una vez que sabemos lo suficiente sobre estadística como para entender qué fórmulas utilizar y qué significan los resultados, la parte de los cálculos es simplemente cuestión de introducir los datos en las ecuaciones que hayamos elegido.

Dado que las estadísticas en sí mismas son relativamente «fáciles» de calcular, Wheelan explica que personas bienintencionadas elaboran estadísticas engañosas constantemente. Señala que muchas de las estadísticas con las que nos encontramos son matemáticamente precisas (si repitieras los cálculos, obtendrías el mismo resultado), pero inexactas en cuanto a los hechos (aunque las cifras sean «correctas», son erróneas). En otras palabras, las cifras resisten un análisis minucioso, pero no explican con precisión una situación.

Por ejemplo, podrías utilizar estadísticas para mostrar una relación convincente [entre...

Resumen de «Naked Statistics»: Cómo reducir el sesgo en los datos

Ahora que hemos analizado algunos de los retos y estrategias para la recopilación de datos, repasaremos el análisis de Wheelan sobre la fiabilidad de los propios datos.

Una de las características más importantes de los datos fiables es que ofrecen una representación fiel de la población que estamos estudiando. Como ya comentamos en la sección dedicada a la estadística inferencial, muchos proyectos de investigación y análisis estadísticos se basan en el muestreo para obtener información sobre una población más amplia. Si los datos recopilados en nuestra muestra no representan con precisión a nuestra población, las estadísticas resultantes no serán fiables. Wheelan destaca dos formas principales de garantizar una muestra representativa:

Muestreo aleatorio: Una muestra verdaderamente aleatoria es ideal para la recopilación de datos. El muestreo aleatorio nos permite tener una confianza razonable en que estamos captando la diversidad de la población subyacente, ya que cualquier individuo tiene las mismas posibilidades que cualquier otro de ser seleccionado. Por lo tanto, la diversidad de la muestra debería ser similar a la de la población. Cuando una muestra refleja con precisión la composición de su población, se denomina «muestra representativa».

Muestras de gran tamaño: Cuanto mayor sea el tamaño de nuestra muestra,...

Ejercicio breve: Analiza tus fuentes de sesgo

Imaginemos el siguiente escenario hipotético de investigación:

Un grupo de investigadores interesados en el efecto del yoga y la meditación sobre el bienestar emocional montó un stand en un gran ashram el último día de un retiro de yoga de una semana de duración. (Su hipótesis nula es que practicar yoga y meditación a diario no tiene ningún impacto en el bienestar emocional). A medida que los participantes abandonan el retiro, muchos se detienen en el stand para rellenar el cuestionario de los investigadores, en el que se les pregunta si creen que el yoga y la meditación tienen un impacto positivo en su bienestar emocional y que valoren su sensación de bienestar emocional hoy en comparación con el primer día del retiro. Utilizando estos datos, los investigadores rechazan su hipótesis nula y publican un artículo titulado: «La práctica diaria de yoga mejora universalmente el bienestar emocional».

¿Qué fuentes de sesgo de selección puedes identificar en este estudio? (Recuerda que el sesgo de selección se produce cuando nuestra muestra no es aleatoria y ciertos subconjuntos de la población están sobrerrepresentados o infrarrepresentados.)